Top methods an algebra 2 tutor uses To teach rational equations effectively

Wiki Article

The Comprehensive Insurance Coverage of Algebra 2 Tutoring: Trick Concepts and Skills for Mastery

Algebra 2 tutoring provides a wide range of important ideas and abilities needed for pupils to attain mastery in maths. This incorporates a comprehensive understanding of polynomial features, complicated numbers, and logarithmic formulas, to name a few. Each subject develops on the previous one, producing a natural structure for problem-solving. The application of these ideas in real-world situations highlights their importance. There stay vital locations that can further boost a pupil's mathematical trip.

Understanding Polynomial Features

How do polynomial functions shape the landscape of algebra? These essential expressions, including variables increased to non-negative integer powers, act as the foundation of numerous algebraic concepts. They can be characterized by their degree, which shows the highest power of the variable, and their coefficients, which identify the feature's actions. Polynomial features exhibit distinctive properties, such as continuity and smoothness, permitting them to model a range of real-world scenarios. Their visual representations include curves that can show numerous behaviors, including intercepts and transforming points. Comprehending polynomial features involves understanding operations such as enhancement, multiplication, reduction, and division, along with factoring methods. This foundational expertise is important for addressing inequalities and equations. By comprehending polynomial features, trainees create essential problem-solving abilities and acquire insight into more intricate mathematical principles, leading the way for advanced research studies in algebra and past.

Grasping Complicated Numbers

Grasping complex numbers is vital for students in Algebra 2, as these numbers prolong the actual number system to resolve formulas that do not have actual services. Understanding their definition and buildings prepares for doing operations with complex numbers properly. This foundational understanding will allow learners to tackle more innovative mathematical principles with self-confidence.

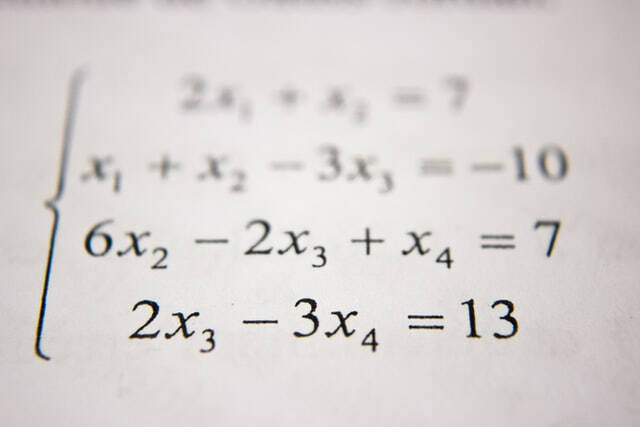
Interpretation and Quality

Intricate numbers, a keystone of innovative algebra, extend the concept of one-dimensional number lines to a two-dimensional aircraft. Specified as numbers of the kind (a + bi ), where (a) and (b) are genuine numbers and (i) stands for the imaginary unit with the home (i ^ 2 = -1 ), these numbers have special properties. The genuine component (a) indicates the straight axis, while the fictional component (b) suggests the upright axis in the complex plane. Secret buildings include their capability to stand for services to polynomial equations that lack real services and their closure under addition, subtraction, division, and multiplication (other than by no) This framework enables a deeper understanding of mathematical ideas and applications across various areas.

Procedures With Complicated Numbers

Workflow with intricate numbers create a crucial facet of algebra that boosts mathematical understanding and problem-solving capacities. Intricate numbers, revealed in the type (a + bi), where (a) and (b) are actual numbers, need specific procedures like addition, subtraction, department, and multiplication.

Addition and reduction include integrating like terms, while reproduction utilizes the distributive residential or commercial property and the truth that (i ^ 2 = -1) Department of complex numbers requires multiplying the numerator and common denominator by the conjugate to remove the fictional component in the . algebra 2 tutor.

These procedures not just strengthen fundamental algebra skills however likewise prepare students for more sophisticated subjects, such as square features and polynomial equations. Mastery of complex number procedures outfits learners with crucial logical tools.

Checking Out Logarithmic Formulas

In the study of logarithmic formulas, recognizing the residential properties of logarithms is crucial for efficient analytical. These homes give the fundamental tools required to manipulate and streamline logarithmic expressions. By grasping these concepts, students can confidently tackle a range of logarithmic equations.

Recognizing Logarithm Characteristics

Logarithm residential properties play an important function in streamlining and solving logarithmic equations, offering a systematic method to comprehending their actions. These homes consist of the quotient, product, and power rules. The item rule mentions that the logarithm of an item is the amount of the logarithms of its aspects. Alternatively, the ratio rule suggests that the logarithm of a ratio is the difference of the logarithms. The power guideline discloses that the logarithm of a number elevated to a backer can be shared as the backer increased by the logarithm of the base. Mastery of these residential properties boosts one's capability to adjust logarithmic expressions, providing a structure for tackling extra complicated formulas and functions encountered in advanced algebra.

Solving Logarithmic Formulas

How can one effectively address logarithmic equations? To deal with these equations, it is essential to utilize properties of logarithms. Initially, one ought to consolidate logarithmic expressions making use of the product, power, and ratio rules. This simplification typically transforms the equation into a more workable type. Next off, transforming logarithmic formulas to their rapid type can disclose the unknown variable. For instance, the equation (log_b(x) = y) translates to (x = b ^ y ) Additionally, examining remedies is necessary to guarantee they do not produce supplementary results, particularly when handling logarithms. By methodically applying these methods, individuals can with confidence browse and resolve logarithmic formulas, enhancing their overall understanding and proficiency of this mathematical concept.

Assessing Sequences and Series

Sequences and series might originally appear complicated, they are essential principles in algebra that disclose patterns and partnerships within numbers. A series is a checklist of numbers set up in a details order, typically specified by a formula or policy. Comprehending the kinds of sequences, such as math and geometric series, permits students to identify the underlying patterns successfully.

On the other hand, a series is the amount of the regards to a series. Analyzing collection involves acknowledging limited and unlimited series, along with calculating their amounts when applicable. Trainees discover crucial strategies, such as making use of solutions for the sum of arithmetic and geometric collection, which simplify right here calculations.

Understanding series and collection equips trainees with vital analytic abilities, enabling them to deal with much more intricate mathematical principles. This foundation is important for their continued success in algebra and higher-level maths.

Addressing Rational Expressions and Formulas

Sensible expressions and equations represent crucial parts of algebra, involving fractions where the numerator and denominator are polynomials. Grasping the addressing of these expressions needs recognizing just how to adjust them efficiently. This includes simplifying expressions by factoring, canceling usual factors, and discovering a common measure when including or deducting sensible expressions.

When resolving reasonable equations, one should isolate the variable, frequently by cross-multiplying to remove the portions. It is very important to examine for extraneous services, as multiplying both sides can introduce worths that do not please the initial formula. On top of that, pupils should know constraints on the variable, as specific values can make the denominator zero, providing the expression undefined.

Comprehending Conic Sections

Conic areas are geometric numbers obtained from the crossway of an aircraft and a dual cone. These sections consist of circles, ellipses, parabolas, and hyperbolas, each identified by distinct residential properties and formulas. Comprehending conic sections is crucial for pupils as they explore the connections in between algebra and geometry.

Circles are specified by a constant range from a center factor, while ellipses arise from a plane puncturing both cones, forming a closed curve. Parabolas emerge from an airplane parallel to the axis of the cone, showing a U-shaped graph. Hyperbolas, on the various other hand, occur when the plane converges both halves of the cone, resulting in 2 unique, open contours.

In Algebra 2, grasping conic areas entails recognizing their conventional formulas, graphing them precisely, and recognizing their crucial features, such as axes, emphases, and vertices. This foundational understanding prepares pupils for more sophisticated mathematical principles.

Applying Graphs and features

Functions and charts function as basic tools in Algebra 2, making it possible for pupils to design partnerships between variables and picture mathematical find principles. Proficiency of these elements permits learners to translate information, determine trends, and make predictions based upon recognized patterns. Pupils check out various sorts of functions, consisting of linear, quadratic, polynomial, reasonable, and exponential, each with distinct characteristics and applications.

Graphing these functions entails comprehending essential features such as asymptotes, slopes, and intercepts, which offer insights right into their actions. Furthermore, students find out to change functions through stretches, representations, and changes, boosting their capacity to manipulate and evaluate visual depictions.

Using features in real-world contexts better solidifies comprehension, as students deal with troubles including earnings margins, population development, and physics formulas. This practical application bridges theoretical understanding with concrete end results, fostering a deeper admiration for the significance of functions and charts in day-to-day life.

Often Asked Inquiries

Just How Can I Boost My Problem-Solving Skills in Algebra 2?

To enhance analytical skills in Algebra 2, one must practice routinely, seek diverse issues, utilize on-line resources, work together with peers, and focus on understanding underlying principles instead of memorizing treatments, fostering much deeper understanding and application.

What Resources Are Advised for Added Algebra 2 Method?

Advised resources for added Algebra 2 practice include online platforms like Khan Academy, books with method troubles, and tutoring services. Participating in math forums can also give varied analytical methods and joint knowing possibilities.

Exist Online Tutoring Options Available for Algebra 2?

Yes, various on the internet tutoring options exist for Algebra 2 (online algebra her response 2). Systems like Khan Academy, Chegg Tutors, and Wyzant deal personalized help, video clip lessons, and interactive exercises, satisfying various learning styles and timetables for students looking for assistance

Just how Do I Plan for Algebra 2 Tests Successfully?

To prepare successfully for Algebra 2 exams, one need to examine essential concepts, method problems on a regular basis, use online sources, create study teams, and take technique tests to identify strengths and weaknesses for targeted improvement.

What Are Typical Misconceptions Pupils Have in Algebra 2?

Trainees typically misconstrue the relevance of foundational concepts, believing they can skip requirements. They might also have a hard time with abstract thinking, perplexing features with formulas, and misunderstanding the role of variables in algebraic expressions.

Understanding complex numbers is essential for pupils in Algebra 2, as these numbers expand the actual number system to solve formulas that lack actual remedies. These operations not just enhance fundamental algebra skills but likewise prepare trainees for more innovative subjects, such as polynomial equations and quadratic functions. Sensible expressions and equations stand for vital elements of algebra, involving fractions where the numerator and denominator are polynomials. In Algebra 2, mastering conic sections includes acknowledging their typical equations, graphing them properly, and identifying their key attributes, such as axes, foci, and vertices. Applying functions in real-world contexts even more strengthens understanding, as trainees take on issues including profit margins, population development, and physics equations.

Report this wiki page